八、 方差分析
F 检验
基于 F 分布的假设检验分布,比较方差或模型整体显著性。
F 分布由两个独立的卡方分布除以各自自由度后相除得到:
F=χ22/df2χ12/df1
F 值越大,说明两组方差差异越显著。
方差齐性检验
用于检验两组或多组数据的 总体方差 是否相等。
F=s22s12(s12>s22)
查 F 分布表,若 F>Fdf1=df2=n−1,α=0.05,则 拒绝 方差齐性假设。
方差分析
用于多个均数比较,简称 ANOVA。
要求:
- 各样本是相互独立的随机样本;
- 各样本来自正态总体;
- 各处理组总体方差相等。
均方 MS: 平方和处以自由度,表示平均变异。SS 作为平方和,是变异的总量。
目的: 检验定量资料(数值变量)中两个或两个以上 总体均数间 差别是否有显著性。
核心思想:变异分解
- 总变异:全部侧量值 Xij 与总体均数 Xˉ 间的差异
- 组间变异:各组的均数 Xiˉ 与总体均数 Xˉ 间的差异
- 组内变异:每组的 j 个原始数据与该组的均数 Xiˉ 间的差异
SS总=SS组间+SS组内
⟹i,j∑(Xij−Xˉ)2=i=1∑K(Xiˉ−Xˉ)2+i,j∑(Xij−Xiˉ)2
ν总=ν组间+ν组内
⟹N−1=(K−1)+(N−K)
变异来源:
- 组间变异:
- 处理因素的不同水平对实验结果的影响 (希望看到的变异)
- 随机误差 (不可避免)
- 组内变异:
因此,通过分解数据的总变异,比较 组间差异是否显著大于组内差异 ,可以回答处理因素对实验结果是否有影响的问题。
完全随机设计的多个样本均数比较
H0:组间变异等于组内变异,此时 处理因素无显著影响。
F=MS组内MS组间=SS组内/ν组内SS组间/ν组间
- F≈1:H0 成立;
- F≫1:H0 不成立。
令
C=N(∑X)2
则
SS总=i,j∑(Xij−Xˉ)2=i,j∑Xi,j2−C
SS组间=i=1∑K(Xiˉ−Xˉ)2=i=1∑Kni(∑Xi)2−C
又
SS组内=SS总−SS组间
故,题目已知 N,K,ni,∑Xi,∑Xi2 ,可以求得 F 的值。
随机区组设计的方差分析
随机区组设计,也叫配伍组设计,指的是将受试对象按性质(控制因素)相同或相近组成 b 个区组,每个区组中的 k 个受试对象分别随机分配到 k 个处理组中。
临床场景:患者病情严重程度不同,按病情分层(区组),每层内随机分配治疗方案。
H0:区组间/处理组间总体均数相等。
- 原则:区组间差别大,区组内差别小;
- 作用:能进一步控制个体差异。
SS总=SS处理+SS配伍+SS误差
ν总=ν处理+ν配伍+ν误差
| 变异来源 | SS | ν | F |
|---|
| 总 | ∑x2−C | N−1 | |
| 处理组间 | ∑i=1kb(∑jxij)2−C | k−1 | MS误差MS处理 |
| 区组间 | ∑j=1bk(∑ixij)2−C | b−1 | MS误差MS配伍 |
| 误差 | SS总−SS处理−SS配伍 | ν总−ν处理−ν配伍 | |
| | | |
以临床实验为例:
- 区组:病情严重程度
- 若 F区组=MS误差MS区组>F(ν区组,ν误差)→拒绝H0 ,则说明病情严重程度确实影响治疗效果;
- 若显著则分层成功控制了混杂因素,提高了检验效能;不影响处理效应。
- 处理:治疗方案
- 若 F处理=MS误差MS处理>F(ν处理,ν误差)→拒绝H0 ,则说明至少有两种治疗方案效果不同;
- 是研究者最关心的结果,决定了处理是否比先前更为有效。
注: 多重比较会导致犯第一类错误的概率增大: α′=1−(1−0.05)m
九、 卡方检验
用于检验分类变量间的关联性或独立性。
四格表资料的卡方检验
研究独立组间数据是否存在差异/变量是否存在关联。
| 治愈 | 未治愈 | 合计 |
|---|
| 新药组 | a | b | a+b |
| 对照组 | c | d | c+d |
| 合计 | a+c | b+d | n |
Pearson 卡方公式
χ2=∑T(A−T)2,ν=1
其中,A 为实际频数,T 为理论频数,ν=1 为自由度。
理论频数计算公式
Tij=nni+n+j
其中,ni+ 和 n+j 分别是相应行和列的周边合计数。
专用公式
χ2=(a+b)(c+d)(a+c)(b+d)(ad−bc)2n
校正公式
χ2=∑T(A−T)2−0.5
χ2=(a+b)(c+d)(a+c)(b+d)(∣ad−bc∣−2n)2n
Fisher 确切概率法
- 获得初始四格表的 ∣a−Ta∣ 和 P 值
- 在四格表边缘合计固定不变情况下,不断减小 a 的值,得到一系列的四格表;
- 算出第 i 个四格表四个格子数据各种组合的概率 Pi 同时得到 ∣a−Ta∣ ;
- 若表 i 的 ∣a−Ta∣≥ 初始表的值,则可以算入总 P 值中。
Pi=a!b!c!d!n!(a+b)!(c+d)!(a+c)!(b+d)!
P=∣ai−Tai∣≥∣a−Ta∣∑Pi
规定:
- 当 n≥40,∀T≥5 时,不需要校正;
- 当 n≥40,∃1<T≤5 时,用校正公式;
- 当 n<40 OR ∀T<1 时,用 Fisher 确切概率法。
配对四格表资料的卡方检验
适用于同一组对象在干预前后的比较,研究其干预效果。不能用来做独立性检验。
| 后测:是 | 后测:否 | 合计 |
|---|
| 前测:是 | a | b | a+b |
| 前测:否 | c | d | c+d |
| 合计 | a+c | b+d | n |
McNemar 检验方法
χ2=b+c(b−c)2,ν=1
当 (b+c)<40 时,使用校正公式
χc2=b+c(∣b−c∣−1)2,ν=1
R×C 列联表的卡方检验
用于多个样本率或多个构成比的比较。其计算公式为
χ2=n(∑ni+n+jAij2−1),ν=(R−1)(C−1)
约束条件:
- ∀Aij≥1
- T≥5 的格子数至少达到 80%(确保大样本)
注意:
- H1 只能认为各总体率有总的区别,不能说明任两个总体率之间有区别;
- 与分类变量的顺序无关,对于有序表不宜使用 χ2 检验。
十、 非参数检验
适用于:
- 不假定总体分布的资料;
- 有序分类变量的资料;
- 总体方差不齐的资料。
秩 Rank: 按一定大小顺序编排后的排名,相同的值采用平均秩。
Wilcoxon 符号秩和检验
适用于:单样本、配对样本。
建立假设检验
- H0:假设配对样本效应相同,则每对变量的差值总体以 0 为中心对称分布,差值中位数 Md=0
- H1:配对效应有差别,差值的总体中位数 Md=0
检验步骤
-
正负分开,分别按差值绝对值由小到大编秩
-
差值为 0 则丢弃,同时样本例数 −1
-
绝对值相等,符号相反则取平均秩次,符号相同取平均或顺次排列;
-
分别求正负秩次之和 T+ T−,取其中任意值为统计量 T
-
当 n≤50 时,可以查 T 界值表
- 若 T 在范围内,则双侧 p>0.05
- 若 T 在范围外,则 p<0.05
- 若等于上下限,则 p=0.05
-
当 n>50 时,无法查表,做近似正态检验:
Z=σT∣T−μT∣−0.5
其中
μT=4n(n+1),σT=24n(n+1)
-
当相同秩次出现过多时,Z 偏小,应该进行校正。
Zc=24n(n+1)(2n+1)−48∑(t3−t)∣T−4n(n+1)∣−0.5
Wilcoxon 两独立样本秩和检验
适用于:两组独立样本(数值、等级型)
建立假设检验
- H0:两独立样本来自分布相同的总体。此时两样本的平均秩次 n1T1,n2T2 相等或很接近。
- H1:两样本代表的总体分布位置有差异。
检验步骤
-
正负分开,分别按差值绝对值由小到大编秩
-
取较小秩和 T=min(T+,T−)
-
n1≤10,n2−n1≤10 时,查 T 临界表;
-
超过范围,做近似正态检验:
Z=σT∣T−μT∣−0.5
其中
μT=2n1(n1+n2+1),σT=12n1n2(n1+n2+1)
-
当相同秩次出现过多时,同样应该进行校正。这里就不写了。
多个独立样本的 H 检验
适用于:多组独立样本(数值、等级型)
又称 Kruskal-Wallis 检验。
建立假设检验
- H0:多组独立样本代表的总体分布相同。
- H1:多组独立样本代表的总体分布位置有差异。
检验步骤
- 将多组数值从小到大统一编秩,将各组分别相加得到每组秩和 Ri(i=1…k)
- 计算检验统计量 H
H=N(N+1)12i=1∑kniRi2−3(N+1)
- 存在结(相同秩次)时(假设第 j 个结的重复次数为 tj)
Hc=1−∑N3−Ntj3−tjH
十一、 线性回归与相关
线性相关
协方差
Cov(X,Y)=E[(X−E[X])(Y−E[Y])]=E[XY]−E[X]E[Y]
-
协方差 >0 时,(X,Y) 分布在区域(1)(3),它们正相关;
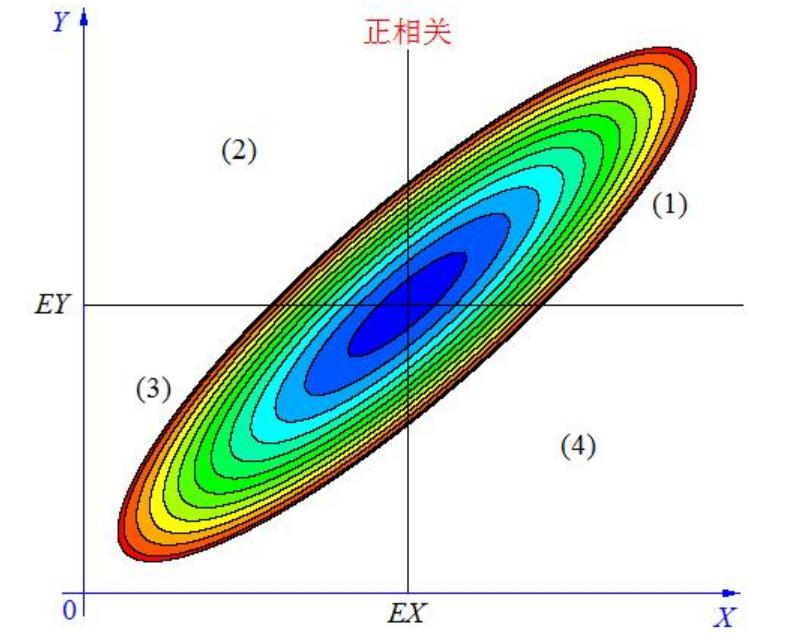
-
协方差 <0 时,(X,Y) 分布在区域(2)(4),它们负相关;
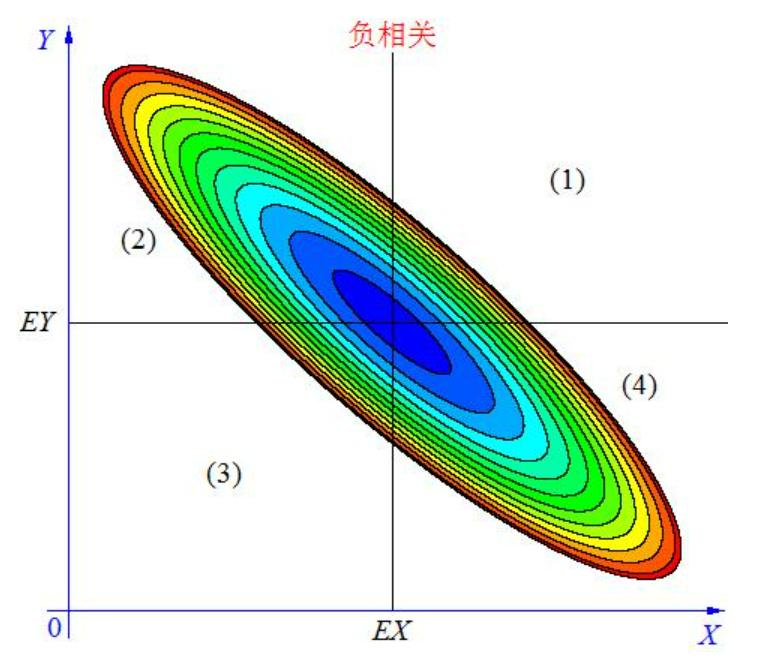
-
协方差 =0 时,它们的分布不相关。
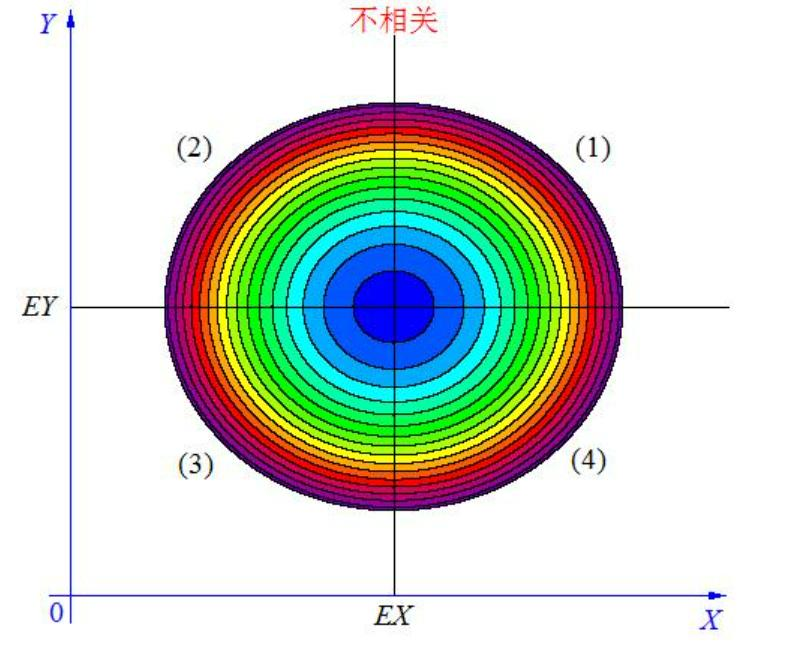
Pearson 积差相关系数
r,表示两数值变量的相关方向(正负)和密切程度(绝对值)
rx,y=Var(X)⋅Var(Y)Cov(X,Y)
其中
Var(X)=E[(X−E[X])2]
这一操作剔除了量纲影响,使其范围限制在 [−1,1] 之间。
相关性的正负与强度
| ∥r∥ | 相关性强度 |
|---|
| (0,0.3] | 较差 |
| (0.3,0.6] | 中度 |
| (0.6,0.8] | 较高 |
| (0.8,1] | 很高 |
相关系数的显著性与假设检验
- 建立假设:
- H0:假设总体相关系数 ρ=0,在此情况下 ∣r∣ 的出现是偶然情况。
- H1:在 ρ=0 情况下,仅凭抽样波动几乎不可能得到 ∣r∣ 这样极端的值,因此拒绝 H0
- 计算统计量:这里以 t 检验较为普遍
t=Sr∣r−0∣
其中 Sr=n−21−r2 为 r 的标准误,自由度 ν=n−2
- 求出临界值 tα/2,ν 得到 P 的关系。
Spearman 秩相关
适用于:
- 不服从双变量正态分布的资料
- 原始数据用等级表示的材料
分析步骤:
- 将变量编秩 RX,RY
- 算出等级相关系数 rs
线性回归
简单线性回归方程
Y^=a+bX
X 是自变量(解释变量),Y 是因变量(结果变量),Y^ 是给定 X 时 Y 的估计值(均值)。
b 是回归系数。
残差平方和
残差 e=Y−Y^
残差平方和
Q=i=1∑n(Yi−Yi^)2=i=1∑n(Y−bXi)2
通过最小二乘法得出使平方和最小的 b
b=Var(X)Cov(X,Y)=∑(X−Xˉ)2∑(X−Xˉ)(Y−Yˉ)
线性回归中总变异的分解
| 变异来源 | SS | ν | F |
|---|
| 总 | ∑(Y−Yˉ)2 | n−1 | |
| 回归 | ∑(Y^−Yˉ)2=Var(X)Cov2(X,Y) | 1 | MS残差MS回归 |
| 残差 | SS总−SS回归 | n−2 | |
线性回归与相关应用的注意事项
自变量 X 既可以是随机变量(称为 Ⅱ 型回归模型,两个变量都服从正态分布),也可以是给定的量(称为 I 型回归模型,在 X 取值固定时 Y 服从正态分布)。
如果 Y 不服从正态分布,在进行回归分析前,应先进行变量的变换以使因变量符合回归分析的要求。
十二、 多元线性回归
多元线性回归
Yi^=b0+b1X1+b2X2+⋯+bmXm
i 表示第 i 组观测值,观测组的数量 n 应该 远大于 参数数量 m。
残差平方和
Q=i=1∑n(Yi−Yi^)2=i=1∑n[Yi−(b0+b1Xi1+b2Xi2+⋯+bmXim)]2
目标是最小化 Q,用最小二乘法逐步得出 b0…m
模型检验-F检验
| 变异来源 | SS | ν |
|---|
| 总 | ∑(Yi−Yiˉ)2 | n−1 |
| 回归 | ∑(Yi^−Yiˉ)2 | m |
| 残差 | Q | n−m−1 |
F=SS残差/(n−m−1)SS回归/m
复相关系数和决定系数
复相关系数 R 表示回归方程中的全部自变量 X 与因变量 Y 的相关密切程度。
R=SS总SS回归,0≤R≤1
决定系数 R2 (回归平方和在总平方和的比重)越接近 1 拟合效果越好。
偏回归系数检验
为了保证每一个自变量都与因变量存在线性关系。
假设:
- H0:bj=0 变量 Xj 与 Y 线性无关。
- H1:bj=0
检验步骤:
-
方差分析-F检验法
剔除 j 以后重新得到回归方程。
F=SS残/(n−m−1)(SS回−SS回(−j))/1
(二者完全等价)
标准化回归系数
bj′=bj(SYSj)
标准化回归系数越大,该自变量对因变量的贡献越大。
多元逐步回归
解决问题:只保留有统计学意义的自变量。
- 向前选择法:从一个自变量开始,对回归平方和最大的自变量做 F 检验,每次引入一个具有统计学意义的自变量,由少到多,直到不具有统计意义的因素不可以引入;
- 向后选择法:先建立一个包含所有自变量的回归方程,对偏回归平方和最小的变量做 F 检验,如果不显著就剔除;
- 逐步选择法:每次向前引入一个新自变量后,重新对已选入的自变量进行检查,引入与剔除交替进行。要求检验水准 α选入≤α剔除
多元线性回归的注意事项
应用条件:“LINE”
- Linear:具有线性关系
- Independent:各观测值相互独立
- Normal:残差 e 服从正态分布
- Equal variance:方差齐性(对于任一组自变量,因变量方差相同)
十三、 Logistic 回归分析
Logistic 回归
因变量为分类变量,概率为 P∈[0,1]
令
Odds=1−PP
logit(P)=ln(Odds)=ln(1−PP)∈(−∞,+∞)
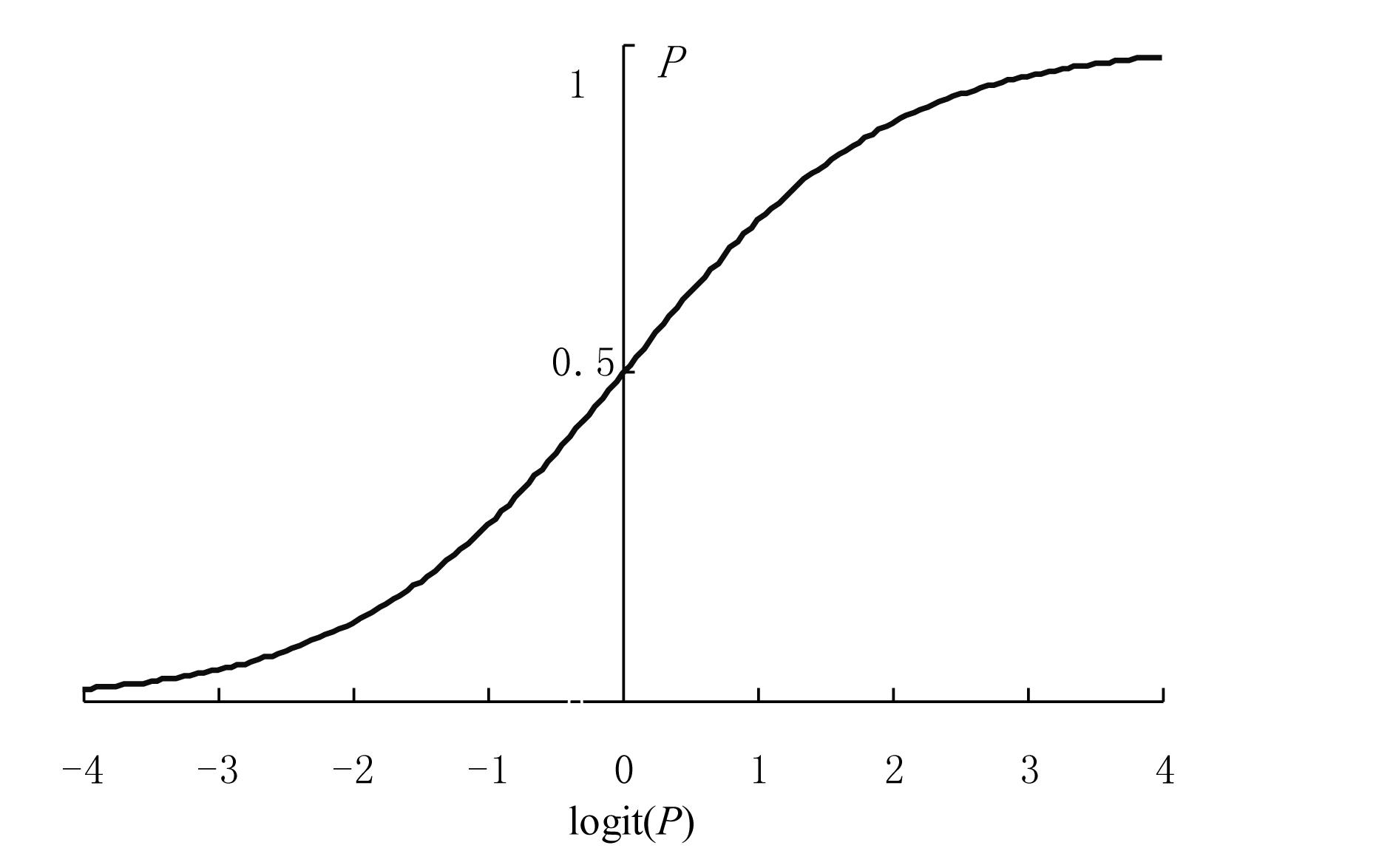
经过 logit 变换, Logistic 回归模型可以表示为如下线性形式:
ln(1−PP)=β0+β1X1+⋯+βmXm
⟹P=1+exp[−(β0+β1X1+⋯+βmXm)]1
Odds Ratio
- 定义: OR=exp[βj(c1−c0)] 表示在其他条件不变的情况下,某个自变量(特征)每增加一个单位时,目标事件发生几率(odds)的变化倍数。
- 公式:如果c1=1, 代表暴露组,c0=0,代表非暴露组,则 OR=exp(βj),
- 当 OR=1:该特征对事件发生没有影响。
- 当 OR>1:该特征增加事件发生概率(保护因素)。
- 当 OR<1:该特征降低事件发生概率(风险因素)。
最大似然估计 MLE
对于第 i 个观测的似然:
Li(β)=PiYi(1−Pi)1−Yi
其中 Pi=1+exp[−(β0+β1Xi1+⋯+βmXim)]1
总似然函数(n 个独立观测):
L(β)=i=1∏nPiYi[1−Pi]1−Yi
目的:找到使得 L(β) 最大的 β,用来估计该模型的参数。
似然比检验 LRT
基于最大似然估计,检验新旧模型的拟合优度,判断新增加的参数是否显著改善了模型。
基本思想:如果简化模型已经足够好,完整模型的似然值不会显著增高。
λ=−2ln(L完整L简化)
分布:假设简化模型的参数个数为 l,完整模型的参数个数为 p,则 λ 近似服从 ν=p−l 的 χ2 分布。
若 λ≥χα,ν2 :则表示新加入的 ν 个自变量对回归有显著的贡献。
Wald 检验
基于最大似然估计,将各参数 βj 的估计值 bj 与 0 比较,检验 βj=0 是否成立。可以用于判断某个参数是否显著地不为某个特定值(通常为0)。
对于大样本资料,
z=SE(bj)bj−0 or χ2=(SE(bj)bj−0)2
服从标准正态分布或 ν=1 的卡方分布。
变量筛选
使用逐步回归法筛选自变量(似然比检验),确定选入水准 α、筛出水准 α出
条件 Logistic 回归
在设计阶段对可能构成混杂的因素进行控制,每个病例匹配1至多个对照,是针对配对病例对照研究的一种分析方法。
Logistic 回归应用及注意事项
应用:可以估计某一因素不同水平下的 ORj 以及近似相对危险度 RRj
| 指标 | 定义 | 公式 |
|---|
| OR (Odds Ratio) | 暴露组患病几率与非暴露组患病几率的比值 | c/da/b=bcad |
| RR (Relative Risk) | 暴露组患病概率与非暴露组患病概率的比值 | c/(c+d)a/(a+b) |
混杂因素的判断标准:
- 与暴露因素相关联;
- 与结局独立相关;
- 不是暴露因素导致结局的中间变量。
十四、 生存分析
基本概念
生存时间: 从规定的观察起点到某重点事件出现所经历的时间间隔;
删失数据: 不知道确切生存时间的数据,右删失数据称为截尾数据 t+
生存数据特点:
- 同时考虑生存结局和生存时间;
- 生存时间可能有删失数据和截尾数据;
- 生存时间往往不服从正态分布。
死亡概率: 死于某段时间的可能性大小
q=某年初观察例数某年内死亡数
当存在删失数据时,分母改成校正观察例数:
期初校正观察例数=期初观察数−21删失例数
相对应,有生存概率 p=1−q
生存率/生存函数: 观察对象的生存时间 T 大于某时刻 t 的概率,用 S^(t) 表示:0≤S^(t)≤1,其定义为
S^(t)=P^(T>t)=观察总例数t时刻存活例数
若有删失数据:需要分段计算生存概率 pj^(j=1,2,⋯,i)
S^(ti)=p1^p2^⋯pi^=S^(ti−1)pi^
风险函数: 生存时间已达到 t 的观察对象在时刻 t 瞬时死亡率,用 h(t) 表示,其定义为
h(t)=Δt→0limΔtP(t≤T<t+Δt∣T≥t)
生存曲线及比较
Kaplan-Meier 生存率曲线
- 将生存时间 ti 按从小到大排序(删失数据在完全数据之后)
- 列出 [ti,ti+1) 的复发数 di 删失数 ci
- 计算复发概率 qi^=nidi 生存概率 pi^=1−qi^
- 计算生存率 S^(ti)=S^(ti−1)pi^
- 计算生存率的标准误
SE[S^(ti)]=S^(ti)tj≤ti∑nj(nj−dj)dj,j=1,2,⋯,i
它不依赖于生存时间服从任何特定的分布假设,而是直接基于实际观察到的生存数据(如删失数据)来估计生存函数,因此是一种 非参数的估计方法 。
Log-rank 检验
又称时序检验,属于非参数检验,不指定生存时间服从特定分布。
H0:不同组别在时间-事件数据上不存在显著差异。
则在 H0 成立时:根据 ti 时的死亡率,可以计算出各组的理论死亡数。
检验统计量 χ2 近似服从自由度 ν=g−1 的 χ2 分布。
χ2=∑Vki[∑dki−∑Tki]2,k=1,2,⋯,g
其中,
- dki 是各组在时间 ti 上的实际死亡数;
- Tki=ninkidi 是各组在时间 ti 上的理论死亡数;
- Vki 是第 k 组的方差估计值。
Breslow 检验
χ2=∑wi2Vki[∑widki−∑wiTki]2,k=1,2,⋯,g
- wi=ni 比 Log-rank 多了一个权重。
Cox 回归
风险函数
h(t,X)=h0(t)exp(β1x1+β2x2+⋯+βmxm)
风险比 Hazard Ratio
表示协变量 Xj 每增加一个单位时,风险函数 h(t,X) 变化的倍数。
HR=exp[βj(c1−c0)]
其中,c1 和 c0 分别表示自变量 Xj 的两个取值。
协变量效应始终 与时间无关。
作用:
- =1:无作用
- >1:危险因子(意义:暴露于该因素会提高事件发生概率)
- <1:保护因子(意义:暴露于该因素会降低事件发生概率)



